When Russia invaded Ukraine four weeks ago, many expected a quick Russian victory. And yet Ukrainians are fighting hard, making Russian advances costly to the invaders. Jan Kofroň and Jakub Stauber argue that the slow Russian progress is unsurprising. Quick victories are rare in modern warfare
Assessing Russian military progress in Ukraine depends on use of a benchmark – which is missing. We lack any real knowledge of pre-war Russian plans, and there have been only a few cases of conventional wars of this type since 1990. Thus, we need to find a different benchmark for comparison.
An alternative benchmark is to compare actual military progress with a formal model of military operations. Stephen Biddle offers such a model in his famous book Military Power: Victory and Defeat in Modern Battle.
Biddle's model focuses on explaining ‘breakthroughs’. The breakthrough is a crucial achievement or milestone. It means the invader has been able to overcome the defender's 'last' defensive positions. The invader's territorial gain is bigger than the depth of the defence. They can freely manoeuvre behind the enemy's line, cutting vital logistical lines of the defender.
Without a breakthrough, the war will turn into a long and bloody campaign of attrition
Without a breakthrough, the war will turn into a long and bloody campaign of attrition. While political goals might be attained with a long war of attrition, invaders usually prefer a quicker and less painful alternative. It is a reasonably safe assumption that this is what Putin intended in his invasion of Ukraine.
The model we use is a simplified version of Biddle's. While a full description, with 11 variables and 9 constants, is beyond the scope of this blog, we summarise the key variables below.
| Variable | Description | Whose choice? | Range in our simulation (min–max) |
|---|---|---|---|
| b | defender troop strength (total direct-fire combat arms personnel in theatre) | defender* | 120–150,000 |
| r | invader troop strength (definition as above) | attacker* | 80–120,000 |
| tb | weighted mean introduction date for defender’s major weapon systems (years) | defender* | 1985–1995 |
| tr | as above, but for the invader | attacker* | 1975–1990 |
| wth | theatre frontage overall (km) | pre-determined | 700–1000 |
| d | depth of the defender’s forward positions (km) | defender | 25–60 |
| vr | velocity of the defender’s rear-area reserve movements (km/day) | defender | 10–50 |
| fr | fraction of the defender’s troops withheld in mobile reserve | defender | 0.2–0.7 |
| fe | fraction of the defender’s forward garrison exposed | defender | 0–0.4 |
| wa | invader’s assault frontage (km) | attacker | 2–10 |
| va | velocity of the invader’s assault at the point of attack (km/day) | attacker | 1–20 |
| Constant _1 | number of invaders one defender can halt when fully reinforced and fully concealed (personnel) | both* | 2–3 |
The impact of different variables on the outcome is complex. We can, however, highlight key relationships between them. Numerical or technological superiority is important, but other variables are more decisive.
For example, deeper defences are much harder to break through, even though this means the defender will likely have to sacrifice some territory. Meanwhile, while one would expect that a higher velocity of reserves would favour the defender, it comes at a price. Too high a velocity might result in high casualties, meaning that reserves do not then arrive at full strength.
The invader might be tempted to proceed as swiftly as possible, especially if trying to win within a narrow window of opportunity. A swift attack, however, means that its forces will be exposed to the defender's fire. If the defender is competent, the invader will experience high losses, making a breakthrough unlikely.
Biddle’s model, of course, operates at a high level of generality. It does not factor in weapon composition or the organisational structures of the opposing forces. At the same time, it makes the model more accessible and applicable even for situations when we have only limited information on the belligerents.
As a result of the ongoing character of the conflict, we have only limited data on the key parameters needed for the model. To overcome this, we decided to simulate thousands of alternative scenarios with randomly varying values of the key variables.
We set up upper and lower bounds for the variables, explained in the table. In the next step, we ran thousands of alternative scenarios to determine possible territorial gains of the invader – here, of course, Russia.
The numbers we decided to employ are deliberately rather favourable to Russians, thus making our simulation rather conservative from a Ukrainian defence point of view. We did not try to account for the impact of the air force. The lacklustre performance of the Russian air force in the first month of the invasion, however, makes this issue rather moot.
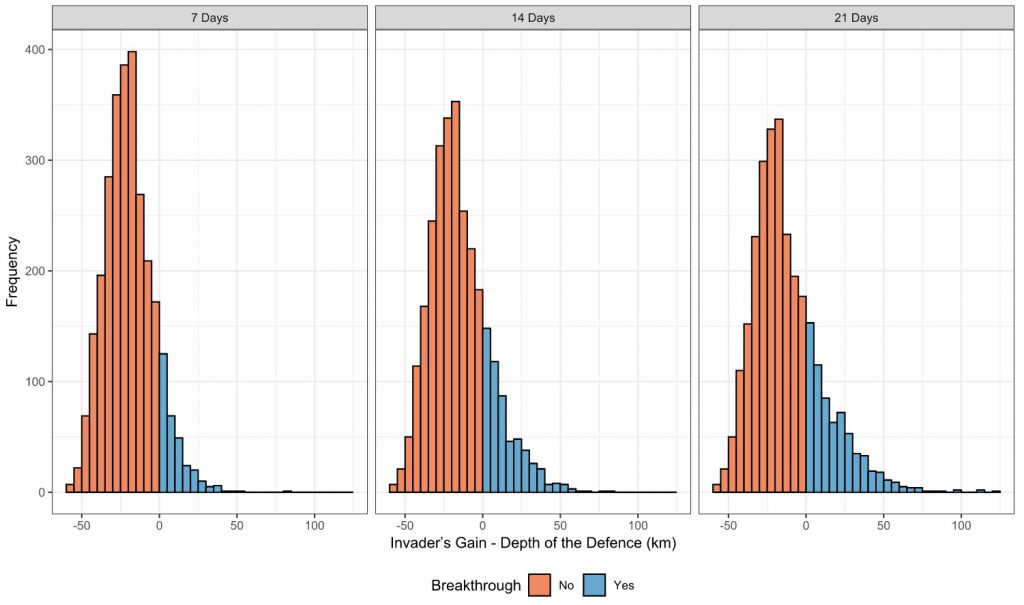
The chart below demonstrates that it seems unlikely the attacker could break through defensive positions within one week. And while there is a much higher chance of a breakthrough after two or three weeks, it remains a risky enterprise.
In addition, we work with a single axis of attack, and do not account for logistical problems or guerrilla-style raids against logistical convoys. Russia, however, tried to advance along several axes in the actual campaign and did not provide enough troops to secure extended logistical lines, thus making its situation even more problematic.
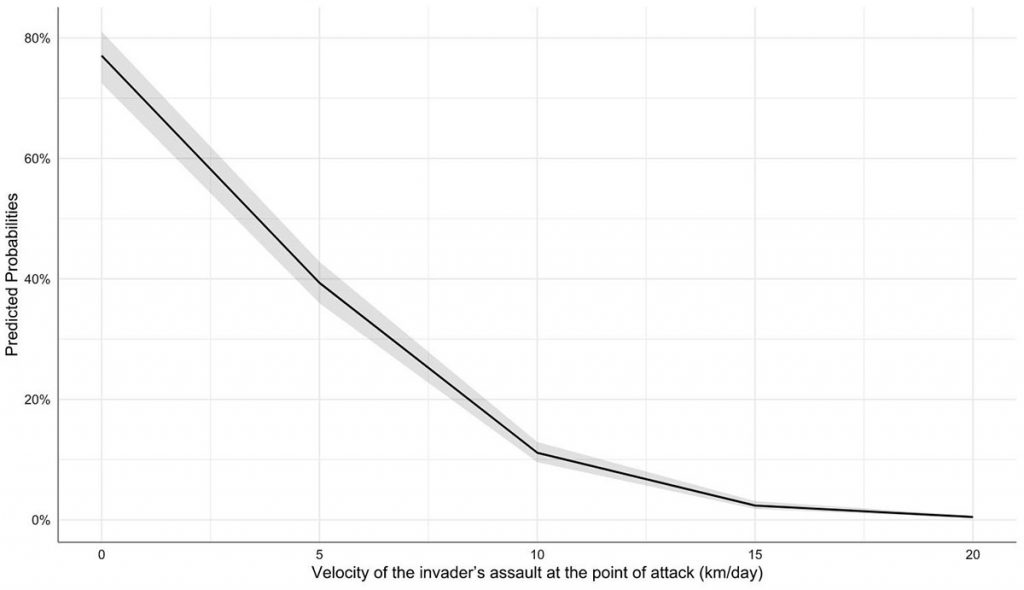
The graph below, meanwhile, is a visual representation of a logit model based on the simulated data for a three-week-long campaign, using all variables as predictors, and the occurrence of a breakthrough as a dependent variable. The key relationship is clear: the higher the attempted velocity of attack, the lower the chance of a breakthrough. A quick victory is hard to achieve in modern warfare.
Russians tried to sprint towards achieving their objectives, assuming that Ukrainians would not fight back. This gave them big territorial gains in the first three days wherever the Ukrainians were unprepared. But once Ukraine established its defence, attempts at quick and massed attacks became counter-productive, if not suicidal.
To some observers (and surely to Putin himself) the slow Russian progress in the past month has been surprising. However, given overconfident Russian tactics and faulty assumptions, the outcome so far fits rather well with the predictions of Biddle's model.
The model fails to consider the importance of morale/commitment. Clearly, if the Ukrainians folded (as they were expected to), then defense in depth does not matter. Similarly, if the attacker is incompetent and/or undermotivated, measured velocity and use of combined arms tactics will not hand them victory.
Second, I do not understand your 2-10 km assault frontage. This is picking a narrow part of the invasion; it misses northeast of Kiev, and the entire southeast and southern areas (where Russia made firmer gains at lower velocities). While you may have attempted to only measure a "portion" of the battle, in this case, especially for Kiev and Moscow, it was a single campaign (not separate, for example, like D-Day and the Italian campaign).